Source: Downloaded from the Internet.

TL;DR

Erwin Schrödinger predicted that the genetic material which encodes the development of living organisms must be large molecules that are stable and also expressive. The first condition ensures the perseverance of the attributes that are transferred to the next generations while the second condition enables the distillation of the whole development plan of an organism in that large molecule which he called an aperiodic crystal whose structure was later discovered and named DNA. In this article, I review Schrodinger’s lectures delivered in 1944 titled “What is life” and make a tiny amendment by connecting it to the theory of Turing Machines, the abstract general computational devices put forward by Alan Turing in 1936.

What is life?

This has been a grand question that humans have asked themselves throughout their existence on earth. People from various perspectives have investigated this question and reached different conclusions some of which can not be merged into a consistent set of characteristic properties that define a living being.

Is there anybody out there? Can you hear us? Are we loud enough?

We, humans, are the most obvious living system that we know with common sense without actually defining what is the exact definition of the term “living”. This human-centric view may be misleading if it leads to a distant-based definition of life that turns the term living into a continuous adjective where something is as much living as it is similar to humans. As soon as we use the word “similar”, we have to be careful that it comes with an implicit metric that judges the similarity of two things. Hence, this self-centric view does not contribute to understanding the meaning of being alive. We need a more universal observer-independent measure. Can such a measure even exist? It is immediately clear that the relevant areas of science are those that do not depend on human constructs and agreed rules. For example, it’s unlikely that psychology or sociology could help much as they mostly concern the emergent concepts and norms in individual or collective behaviors. Hence, we need to resort to more fundamental areas such as physics and mathematics.

Schrodinger’s aperiodic crystal

One of the most known efforts in explaining the boundary between living and non-living things is the lecture series by Erwin Schrödinger in 1944 which was later collected in a book titled “What Is Life? The Physical Aspect of the Living Cell”. As expected from the author, the arguments in this lecture originate from physics and chemistry. I call Schrodinger’s approach “normative” as what he answers is

What it takes for an object to be alive in a universe where the existing phsyical laws hold?

I call this approach normative as it serves as a predictor rather than only explaining what is known so far. Note that the structure of the genetic material of a cell was not known at the time of Schrodinger’s lectures. It is astonishing that his approach laid theoretical description and prediction of how genetic information has to be stored which was later acknowledged by the discoverers of DNA double helix structure in 1953. Before we start looking into his theory, I want to emphasize what Schrodinger wrote in the preface of his book about noblesse oblige figuratively referring to the unwritten rule in the scientific community that one is expected not to write on any topic of which he is not a master. In an immensely complex problem such as life, cross-disciplinary knowledge is necessary which made him renounce the noblesse and its ensuing obligation with the following excuse:

We have inherited from our forefathers the keen longing for unified, all-embracing knowledge. The very name given to the highest institutions of learning reminds us, that from antiquity and throughout many centuries the universal aspect has been the only one to be given full credit. But the spread, both in width and depth, of the multifarious branches of knowledge during the last hundred-odd years has confronted us with a queer dilemma. We feel clearly that we are only now beginning to acquire reliable material for welding together the sum total of all that is known into a whole; but, on the other hand, it has become next to impossible for a single mind fully to command more than a small specialized portion of it.

This is alarming as it implies that some of the biggest questions are indeed unsolvable. I don’t go into more details about how this can be proved here not to hurt the cohesion of this article but will hopefully expand it in another article with the tentative title

On the human-unsolvability of hard questions?

Let’s get back to Schrodinger’s lectures.

Less repetative patterns can store more information which is needed to encode a living organism.

The lower-boundedness of the size of living things

One of the first questions that arise when investigating the concept of being alive is the size of living things. Accepting that everything in the physical world is governed by strict physical laws, Schrodinger argues that living things cannot be so small. More precisely, they have to be large enough such that they are not affected by a single or a few atoms. This argument has this implicit assumption for the definition of life that a living thing has an orderly structure and also interacts with orderly things. We know from statistical physics that atoms move almost randomly (heat movement) when observed individually, and physical laws start to appear in the collaboration of an enormously large number of them. Hence, anything consisting of a few atoms will not be able to produce, perceive or interact with orderly things.

An example of particular interest is the measurement device composed of a light object suspended by a long thin fiber in equilibrium which is used by physicists to measure weak forces that deflect it from its position of equilibrium. Trying to increase the accuracy of measurement by increasing the length of the fiber of making the suspended object lighter meets a limit where the measurement becomes sensitive to the heat motion of the molecules in its surroundings which makes the device useless. Our perception organs are also measurement devices and have to be large enough to measure the statistical behavior of molecules; otherwise, they will be perplexed by the Brownian impact of them which our processing unit (brain) cannot make any sense of. As a rule of thumb, the accuracy of physical laws is within the order of $1/\sqrt{n}$ for $n$ being the number of co-operating particles. This immediately suggests that an organism has to have a gross structure to be able to expect a lawful world. The use of X-ray and measuring the mutation rate gave a lower upper bound for the size of a gene in the order of thousands of atoms.

The smaller an organism becomes, less certain it would be about the laws of nature.

The mutation is the working ground for evolution. It is indispensable to differentiate between the randomness in the genotype to phenotype process and the mutation in the genotype. The former results in the distribution of the phenotype with connected support while the latter leads to phenotypes values far from the distribution of non-mutated values without observing the intermediate values. Thus, the discontinuoity is the key sign of genetic mutation. It is important that mutation must be a rare event otherwise the species may vanish before being evolved.

The reconciliation of gene sizes and their regular activities

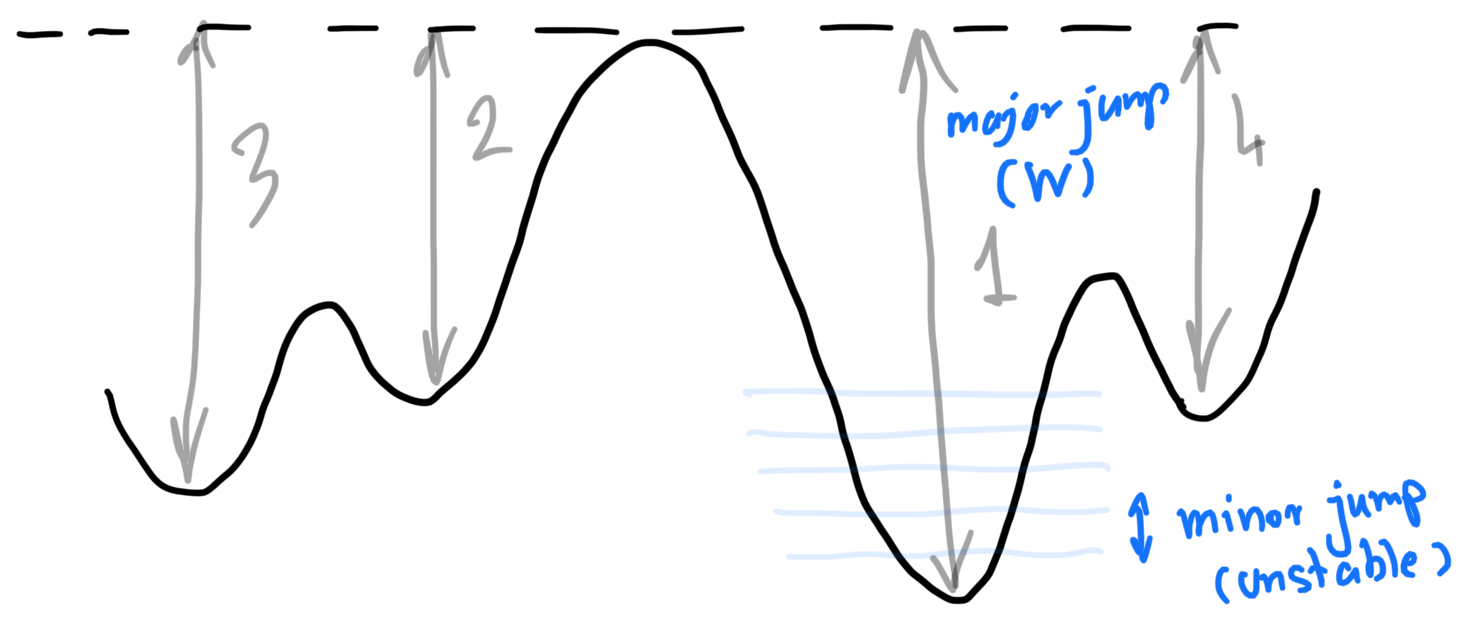
It is historically observed that hereditary attributes are preserved over centuries. This might look in contrast with the fact the gene which encodes that attribute is small enough to be affected by Brownian heat motion. The key is in the concept of discrete energy and equilibrium. Quantum theory predicts discrete levels of energy for atoms. In a more general setting, the molecules which are formed by a few atoms can take only a discrete finite set of states. A certain amount of energy has to be given to the molecule to change its state into a higher energy state whose structure is significantly different. This suggests that the gene (and possibly the entire genetic material) is a molecule whose stability is caused by being at the energy equilibrium.

Less repetative patterns can store more information which is needed to encode a living organism.

There is a large energy barrier that has to be passed to move from this state to the adjacent lower or higher energy levels; a wall that is too high for the energy of heat motion to be strong enough to climb. I want to draw attention to the probabilistic nature of statements in small-scale physics. One way to facilitate the quantum jump of a molecule from one state to another is by increasing the temperate which lead to more energetic heat motion in its surrounding. The effect is though not deterministic. It increases the chance of the occurrence of such a jump which, due to the ergodicity of the process, can be measured as the time it takes until that jump occurs. That time is a random variable (remember everything is probabilistic!) whose mean is empirically observed to follow an exponential rule:

which implies the average time it takes to change the ratio of the needed energy to the energy supplied by the surrounding heat bath. Whan a jump occurs, an isomer of the molecule is obtained that is called an allele for that location (locus) on the chromosome.

Predicting the existence of DNA

It is impressive that Schrodinger’s was able to predict the structure of the genetic material from just a few principles that can be listed as

• The genetic information must be stable enough to be transmitted from generation to generation.
• The genetic material must be information-wise rich to encode all the complex processes that are needed for the development of an organism.

The first point is only possible if the genome is some sort of a molecule where the atoms are connected by Heitler-London bonds. Quantum theory explains that such structures are stable enough that heat motion does not change them into new stable mutants, called isomere. Changing these molecules to new stable ones requires explosion-like energy discharge in reactions such as ionization in the proximity of the molecule (< 10 atomic distance>). This energy barrier is important for the existence of life because it makes the mutation a rare event. If we categorize the state of matters concerning how strong their atoms are connected together, one could see that molecules, crystals, and solid belong to the same category while liquid and gaseous matters fall into another category. The key distinctive factor is Discontinuity which I dare to connect directly to “interestingness” not only in biology but also in other areas of science and mathematics which I summarise in the following quote from an unknown intellect:

Continuity is boring!

It seems that things become interesting when there is some notion of discontinuity in their state. In the abovementioned categorization, there is a certain temperature, known as the melting temperature, in which the crystal changes its state while the members of the second category show a continuous change of state with temperature from one state to another.

The second principle behind Schrodinger’s prediction of the DNA structure is well supported by the algorithmic information theory. Unlike usual crystals which are formed by repeating the same pattern in three dimensions, again and again, the genetic molecule must be aperiodic to allow encoding the accommodate the information content needed to build a complex organism. It is indeed in such structure that every group of atoms (or even every single atom) can play a distinct role as Schrodinger explicates as

We believe a gene - or perhaps the whole chromosome fibre - to be an aperiodic solid.

which is famously known as aperiodic crystal in his theory of life. This is exactly what makes genes responsible for different attributes of a living organism.

Death = Equilibrium

What is the characteristic feature of life? One makes us, as living organisms, different from, e.g. an hourglass? It seems the key is in the concept of equilibrium. Non-living things tend to settle after a relatively short time in some steady (non-moving) state while living things “keep going” and exchange material and energy with their surrounding. This phenomenon is explained by the second law of thermodynamics which states all non-alive isolated systems tend towards a permanent state called “thermodynamical equilibrium” or “maximum entropy” in which no observable event occurs. Being alive can be seen as evading this equilibrium. It seems the living organisms evade this death state by exchanging things with their environment in a process known as metabolism. However, the material is not the essence of metabolism as there is no difference between the atoms within the organism and those outside its boundary. What actually matters is a concept called entropy, which despite being often introduced in various domains as a hazy concept, is a measurable physical quantity as a function of heat and temperature. We are particularly interested in the statistical notion of entropy established by Boltzmann and Gibbs expressed by

where $k$ is the Boltzmann constant and $D$ is a measure of atomic disorder. Technical details aside, the second law of thermodynamics formulates the natural tendency of things to approach the chaotic state (maximum entropy).

Feeding on negative entropy

The theory of negative entropy states that living organisms evade the maximum entropy state by feeding on the orderliness (negative entropy) of their environment. This is, for example, seen in the higher animals whose food consists of complicated organic compounds (low entropy) which they return to the environment in a degraded form (higher entropy). Living organisms get rid of the surplus entropy via another mechanism which is giving heat to their surrounding. This heat must be compensated via the energy they receive from food and other sources, e.g. sunlight. Schrodinger goes even one step further and argues a parallelism between the intensity of life and the body temperature with the idea that animals with higher body temperature get rid of their entropy at a quicker rate and are consequently capable of intenser life which I would rather call

Dancing around the death equilibrium wit higher frequency!

Is Life based on the Laws of Physics?

All physical laws are statistical and the degree of uncertainty in their prediction increases with temperature. Statistical physics explains how such laws can emerge from the chaotic behavior of atoms (“Order from disorder”). The events that occur in the life cycle of an organism exhibit significant regularity caused by notable orderliness which is controlled by a relatively small fraction of its atoms within every cell of its body called genes (Order from order). The ability of the living organism in sucking orderliness from its surrounding seems to be connected with this aperiodic crystal, the chromosome molecule. The lifecycle of an organism cannot be explained by statistical physics where the laws of Physics emerge from the chaotic interaction of atoms not a well-ordered configuration of them. This phenomenon is known as the lack of individual determination which implies the faith of one molecule or atom is randomly determined as a result of Brownian-like events at atomic scales such as heat motion.

This is fundamentally different than the situation in biology where a single copy of the molecule (the DNA of the fertilized egg) gives rise to a sequence of orderly events throughout the development of the organism. Even though the DNA molecules are copied and distributed all over the body of higher animals, their total number, e.g. $10^14$ will in volume be less than a tiny drop of liquid. Considering every cell in an adult animal, the behavior of the cell seems to be governed by deterministic mechanisms not probabilistic ones even though it is governed by only a single copy of the DNA molecule.

Two aforementioned mechanisms that produce order correspond to two types of physical laws, Dynamical and Statistical which are connected in a short article by our beloved Max Planck, titled “Dynamische und Statistische Gesetzmassigkei”. Planck argues in this article that statistical laws that govern large-scale phenomena are controlled by dynamical laws governing small-scale events such as the interactions among single atoms and molecules.

Nernst’s Law

In the dichotomy of statistical and dynamical laws of Physics, the transition from one to another is possible under a certain condition determined by Quantum theory as absolute zero temperature. It is in this temperature that heat motion stops and ceases to have any effect on physical events. This fact was shown empirically by Walther Nernst’s famous “Heat Theorem” also known as the Third Law of Thermodynamics. Quantum theory rationalizes this empirical observation and also predicts that there is a non-zero temperature in which the heat motion effect is practically negligible on a physical system. This temperature can be even as high as the room temperature for systems such as a clock. The same situation holds for the aperiodic crystal by thinking of them as the cogs of a living organism. It is astonishing that unlike in a clock, these cogs are not human-made.

DNA as a Turing Machine

Let’s accept for now that genes are the programs that encode the development of the living organism which are physically implemented as a form of stable molecules. I emphasized the term development to give the impression that, in this view, genes are not only a list of attributes. They are recipes for building the organism from scratch. One could see the gene as a program that contains the code to produce an attribute and also the instruction on how to run that code. Schrodinger’s states more or less the same view:

What we wish to illustrate is simply that with the molecular picture of the gene it is no longer inconceivable that the miniature code should precisely correspond with a highly complicated and specified plan of development and should somehow contain the means to put it into operation.

This suggests an interesting view to see the genetic molecule as a Turing Machine (TM), the abstract model for general computing devices. The big genetic molecule serves as both the program to run and also the Turing machine to run it. As stated, the Turing machine itself can also be encoded in the program together with the code it’s supposed to run. One could see this as bundling the C++ compiler together with the C programs that is supposed to run on a computer. However, a universal machine is still needed to run this bundle. That’s where the concept of the Universal Turing Machine (UTM) comes into play; a machine that is capable of running every other Turing Machine. With some imprecision, one could see the laws of physics (at least in the spatial context of this planet/universe) as the UTM that runs every TM including the special one of our interest, i.e. genes.

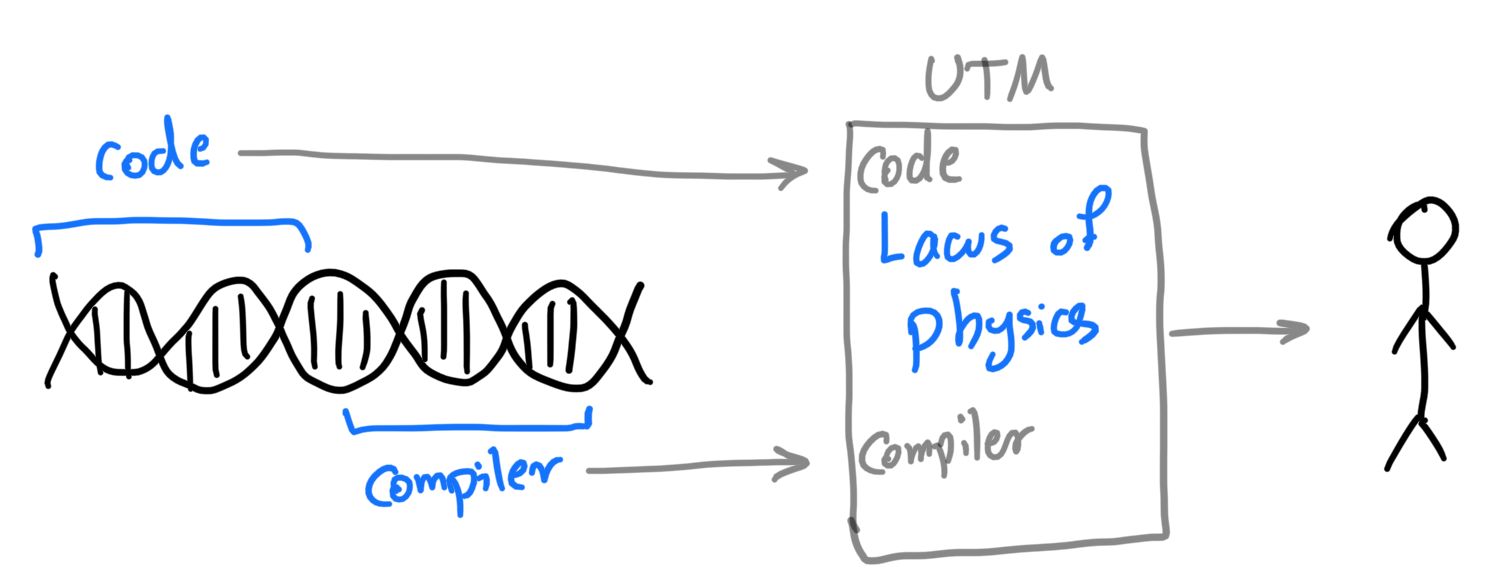
Genes as Turing Machines which are run by the laws of Physics (a Universal Turing Machine) to produce a living organism.